 Histograma y la tabla de frecuencias permiten visualizar estos dos aspectos de un conjunto de datos, y además muestran la forma en que los datos se distribuyen dentro de su rango de variación. De manera específica, el histograma es una representación gráfica, en forma de barras, de la distribución de un conjunto de datos o una variable, donde los datos se clasifican por su magnitud en cierto número de grupos o clases, y cada clase es representada por una barra, cuya longitud es proporcional a la frecuencia de los valores representados. Por lo general, el eje horizontal está formado por una escala numérica para mostrar la magnitud de los datos; mientras que en el eje vertical se representan las frecuencias.
Histograma y la tabla de frecuencias permiten visualizar estos dos aspectos de un conjunto de datos, y además muestran la forma en que los datos se distribuyen dentro de su rango de variación. De manera específica, el histograma es una representación gráfica, en forma de barras, de la distribución de un conjunto de datos o una variable, donde los datos se clasifican por su magnitud en cierto número de grupos o clases, y cada clase es representada por una barra, cuya longitud es proporcional a la frecuencia de los valores representados. Por lo general, el eje horizontal está formado por una escala numérica para mostrar la magnitud de los datos; mientras que en el eje vertical se representan las frecuencias. Comúnmente el histograma se obtiene a partir de la tabla de frecuencias. Para obtener ésta, se determina la marca de clase o numero de clase utilizando la regla de Sturgess, señala que el numero de clase es igual:
Comúnmente el histograma se obtiene a partir de la tabla de frecuencias. Para obtener ésta, se determina la marca de clase o numero de clase utilizando la regla de Sturgess, señala que el numero de clase es igual:MC: (3,3* log10(n) ) + 1
para el caso del grosor de los discos se determina de esta manera:
MC: (3.3* log10(125) ) + 1 = 7,9 = 8 es decir que se forma ocho clase como lo muestra el ejemplo de la tabla 2.2(abajo)
Se recomienda que el numero de clase sea de 5 a 15.
2. paso determina el rango de los valores
Rango= valor max - valor min
para este caso el máximo es: 1.25 y el valor mínimo es : 1.11
Rango: 1.25 - 1.11 = 0.15
3. hallar el ANCHO, con este vas a determinar o construir el rango dentro de la tabla de frecuencia que es
Ancho= Rango/MC
Por ejemplo:
Ancho= 0.15/8 = 0.02
para comenzar a construir nuestro rango escogemos el valor mínimo de nuestros datos que es 1.10
y sumaremos el valor mínimo mas el ancho
1.10 + 0.02 = 1.12 es decir que la primera clase representa a los datos con magnitud entre 1.10 y 1.12
luego el resultado de nuestro primer rango aplicaremos lo mismo
1.12 + 0.02= 1.14
la magnitud esta entre 1.12 - 1.14
continuamos de esta manera hasta obtener todos los 8 clases como lo muestra la tabla 2.2
que el ultimo resultado es igual 1.24 - 1.26
4. paso determinar la frecuencia absoluta que es hallar cuantos valores caen dentro del rango obtenido en el paso 3.
por ejemplo como lo muestra la tabla 2.2
nuestro primer rango es 1.10 a 1.12 al buscar en la tabla 2.1 que valores caen dentro de este se encuentra tres valores que están dentro de este rango es decir que la frecuencia absoluta sera 3 y así sucesivamente para todos.
5. paso hallar la frecuencia relativa que es:
FR= f absoluta / n * 100
6. paso hallar la frecuencia acumulada.
el primer dato de la frecuencia acumulada es el mismo dato de la frecuencia relativa siempre ( observar el cuadro) entonces una vez que tengas esto vas a sumar la frecuencia acumulada que tienes con el segundo dato de la frecuencia relativa es decir 2.4 + 6.8 = 8.8 % que es nuestro segundo dato de la frecuencia acumulada esto consiste como una suma en z...
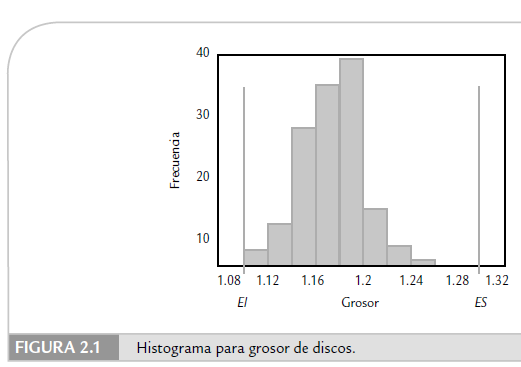
Si en el histograma de la figura 2.1 (se insertan las especificaciones (1.10 y 1.30) para el grosor del disco, se observa que la variación de los datos (amplitud del histograma) es un poco menor que las especificaciones. Pero, con respecto a 1.20, que es el grosor óptimo, el proceso está moderadamente descentrado a la izquierda, como ya se había visto cuando se calculó la media. Además, el grosor de los discos no es satisfactorio, ya que la orilla izquierda del histograma debería estar alejada de la especificación inferior (EI = 1.10), lo cual no ocurre. Cabe comentar que aunque no hay ningún dato por debajo de la EI, no se debe perder de vista que el estudio se hace a partir de una muestra, por lo tanto, si se continúa tomando datos es casi seguro que se encontrarán mediciones fuera, como lo sugiere la prolongación de la cola izquierda de la curva imaginaria que suaviza al histograma. Con base en lo anterior, la primera acción que se habría de ejecutar para mejorar la capacidad del proceso de inyección de discos es mejorar su centrado.
A través del ejemplo anterior queda claro que el histograma ayuda a ver la tendencia central de los datos, facilita el entendimiento de la variabilidad y favorece el pensamiento estadístico, ya que de un solo vistazo se logra tener una idea acerca de la capacidad de un proceso, se evitan tomar decisiones sólo apoyándose en la media y se detectan datos raros y formas especiales de la distribución de los datos. Estos detalles de la interpretación del histograma los veremos con mayor profundidad a continuación.
Interpretación del histograma
Cuando un histograma se construye de manera correcta, es resultado de un número suficiente de datos (de preferencia más de 100), y éstos son representativos del estado del proceso durante el periodo de interés; entonces, se recomienda considerar los siguientes puntos en la interpretación del histograma
1. Observar la tendencia central de los datos. Localizar en el eje horizontal o escala de medición las barras con mayores frecuencias. En el histograma de la figura 2.1, una parte sustancial de las mediciones se localiza entre 1.14 y 1.20 mm.
2. Estudiar el centrado del proceso. Para ello, es necesario apoyarse en el punto anterior y observar la posición central del cuerpo del histograma con respecto a la calidad óptima y a las especificaciones. Por ejemplo, en la figura 2.2 incisos a) y c) se muestran procesos centrados, el primero presenta poca variabilidad, pero en el segundo ocurre lo contrario. Mientras que en los incisos b) y d) se observan procesos descentrados, el primero con poca variabilidad y el segundo con mucha. Aun cuando se cumplan las especificaciones, si el proceso no está centrado, la calidad que se produce no es adecuada, ya que entre más se aleje del óptimo más mala calidad se tendrá. Por ello, en caso de tener un proceso descentrado se procede a realizar los ajustes o cambios necesarios para centrar el proceso.
3. Examinar la variabilidad del proceso. Consiste en comparar la amplitud de las especificaciones con el ancho del histograma. Para considerar que la dispersión no es demasiada, el ancho del histograma debe caber de forma holgada en las especificaciones. En la figura 2.2 incisos a) y b) hay poca variación, mientras que en los incisos c) y d) ocurre lo contrario.
4. Analizar la forma del histograma. Al observar un histograma considerar que la forma de distribución de campana es la que más se da en salidas de proceso y tiene características similares a la distribución normal figura 2.2 a), b), c) y d). Es frecuente que cuando la distribución no es de este tipo sea la señal de un hecho importante que está ocurriendo en el proceso y que tiene un efecto negativo en la calidad. Por ello, es necesario revisar si la forma del histograma es muy diferente a la de campana. Algunas de las formas típicas que no coinciden con una distribución de campana, son las siguientes:









0 comentarios:
Publicar un comentario